昨年、「林先生の痛快!生きざま大辞典」という番組で、
228という驚異的なIQを記録したマリリン・ボス・サヴァントの「モンティ・ホール問題」について取り上げていました。
モンティ・ホール問題とは?
モンティホールという司会者がやっていた番組のクイズで三択問題がありました。
ルールや流れは以下の通り。
- 扉が3つ(A、B、C)あり、正解の扉は一つで景品がある
- 残り2つのハズレの扉にはヤギがいる。
- 回答者は扉(図例ではA)を選ぶ。
- 司会者は選ばれていない扉のどちらかを空ける。(図例ではC)
- (C)にハズレのヤギがいた場合、(A)が正解の可能性があるのでゲームは続行。
- ここで、回答者は最初に選んだ(A)を、残ったもう一つ(B)に変更する事ができる。
- さあ、どうする?

マリリン・ボス・サヴァントの回答
当時、彼女が執筆していたコラムに
これを変えた方が良いのか、変えない方が良いのか、の質問があったところ、
回答は「変えた方が良いに決まっている」と答えたそうです。
ちなみに、ボクはテレビを見ていて思わず「なんでだよ!」と突っ込んでしまいました(汗)
どうして、最初に選んだ扉を変えた方が良いのか?
数学が出来る人は、計算式などですんなり理解できるらしいのですが、
自分は計算式見てもさっぱり理解できません。
そこで、理屈を要約すると以下の通りなのだそうです。
- 最初に選んだ「A」は3分の1の確率で、状況が変わっても確率は変わらない。
- 「B」と「C」は合計で3分の2の確率。これも状況が変わっても確率は変わらない。
- すると、「C」が消えた場合、残った「B」だけで3分の2の確率が残る。重要!
- つまり「A」と比べて「B」は確率が2倍。
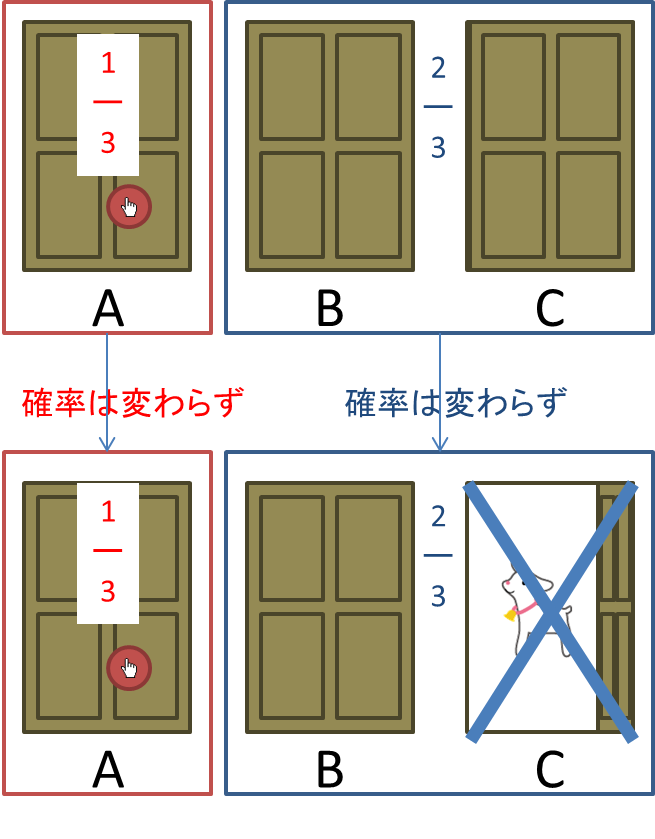
「選択した扉(上記赤枠)」と、「選択していない扉グループ(青枠)」で切り分けて
「選択していない扉グループ」の一つがハズレと分かれば、
「選択していない扉グループ」の残りの一つに変える方が確率は高いのだそうです。
普通、二つで3分の2であった確率は一つに減れば3分の1に半減すると考えるじゃないですか?
でも、計算をちゃんと行うと、残った一つも3分の2のままになるそうなのです。
実際にコンピュータで何万回とテストしたところ、
最後に選択肢を変えた方がおよそ2倍の正解だったそうです。
こういうもんだよと教えられても、素直になれない駄々っ子になった気分ですが、
これが数学の面白さというか奥深さなのかもしれません。
モンティ・ホール問題は、前向きに変化する方が成功しやすい証明なのかも。
商売の現場では、やり方をコロコロ変えて大失敗した事例は多く、
最初に決めた事を押し通す事が時として必要に見えます。
ですが、このモンティ・ホール問題を考えると、
そうとも言えないと思えてきます。
「ハズレの扉」はマーケットの変化という形でゆっくり開いていきます。
どうやら「C」というやり方はハズレのようだ、と感じたら、
「良かったー。Aが当たるかも」と守りに入るのではなく、
前を向き、確率の高い「B」への変更を考え始めるのは悪くないという事でしょう。
今まで上手くいったやり方だけでなく、
あまり考えていなかった「グロウニッチの活用」はいかがでしょうか?(笑)